二进制转化为十进制的简易方法（掌握二进制转化为十进制的技巧，轻松解读数字编码）

二进制（Binary）和十进制（Decimal）是计算机中常用的数字编码方式。掌握二进制转化为十进制的方法，有助于我们理解计算机中的数字表示和运算过程。本文将介绍一种简易的方法，帮助读者轻松将二进制数转化为十进制数。

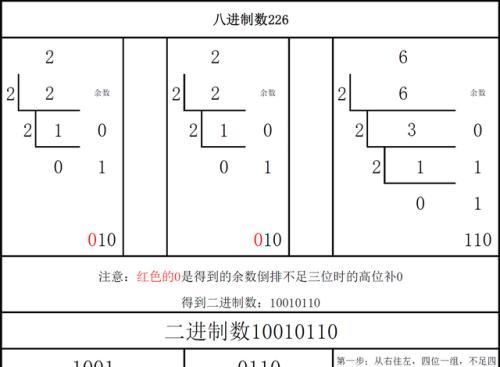
什么是二进制和十进制

二进制是一种由0和1组成的数字编码方式，用于计算机中表示和存储数字。而十进制是我们日常生活中常用的编码方式，使用0到9这10个数字。了解二进制和十进制的基本概念是学习转换方法的前提。

二进制数的位权与权重

在转化二进制数为十进制数时，需要了解每一位上的位权与权重。二进制数的每一位都代表着一个2的幂次方。例如，对于二进制数1101，从右往左，第一位为2^0，第二位为2^1，第三位为2^2，第四位为2^3。

转换规则的基本思路

将二进制数转化为十进制数的基本思路是，将每一位的值乘以对应位权的权重，然后将所有结果相加。这样，就可以得到转换后的十进制数。

从右向左进行转换

二进制数从右往左依次为低位到高位，我们可以从最低位开始转换为十进制数。将第一位乘以2的0次方，第二位乘以2的1次方，以此类推。

示例演示：将二进制1101转化为十进制

以二进制数1101为例，从右往左进行转换，第一位为1乘以2^0，第二位为0乘以2^1，第三位为1乘以2^2，第四位为1乘以2^3。将所有结果相加得到十进制数13。

小数点的位置和转换方法

当二进制数含有小数点时，需要注意小数点的位置与对应的转换方法。小数点右侧的每一位都代表着一个2的负幂次方。

示例演示：将二进制101.11转化为十进制

以二进制数101.11为例，整数部分从右往左转换为十进制数，小数部分从左往右转换为十进制数。将所有结果相加得到十进制数5.75。

注意二进制数的合法性

在进行转换时，需要确保输入的二进制数是合法的。二进制数中只能包含0和1，且小数部分必须以0或1结尾。

负数的二进制转换

对于负数的二进制转换，通常使用补码表示。将负数的绝对值转化为二进制，然后对每一位取反，再加一即可。

转换方法在计算机中的应用

掌握二进制转化为十进制的方法，有助于理解计算机中数字的存储和运算过程。在计算机科学和信息技术领域中，这一方法被广泛应用。

二进制转化为十进制的实际应用场景

在网络通信、数据存储和处理等领域，需要将二进制数转化为十进制数进行进一步的计算和操作。掌握这一转化方法有助于提高工作效率。

继续学习更高级的数字编码方式

除了二进制和十进制，还存在其他数字编码方式，如八进制和十六进制。掌握二进制转化为十进制的方法，为学习更高级的数字编码方式打下基础。

理解数字编码的深层含义

数字编码是计算机科学中的基础知识，理解其背后的原理和含义，有助于我们更深入地理解计算机的运作方式。

不同进制间的转换方法

除了将二进制转化为十进制，还可以将十进制转化为二进制、八进制或十六进制。掌握不同进制间的转换方法，有助于解决实际问题和进行更灵活的数值表示。

掌握二进制转化为十进制的方法，轻松应对数字编码问题

通过本文介绍的简易方法，读者可以轻松掌握将二进制数转化为十进制数的技巧。这一技能在计算机科学和信息技术领域具有重要意义，帮助我们更好地理解和应用数字编码。通过不断练习和实践，我们可以在二进制和十进制之间自如地转换，更好地理解计算机中的数字表示。

转载请注明来自数码俱乐部，本文标题：《二进制转化为十进制的简易方法（掌握二进制转化为十进制的技巧，轻松解读数字编码）》

标签：二进制转化为十进制