深入理解数学复数的基本知识（探索数学复数的性质、运算及应用）

数学复数是由实数和虚数构成的一个数集，广泛应用于物理学、电工学、信号处理等领域。本文将深入探讨数学复数的基本概念、性质、运算规则以及其在实际问题中的应用，帮助读者更好地理解和应用数学复数。

1.什么是数学复数

数学复数由实部和虚部构成，可以表示为a+bi的形式，其中a为实部，b为虚部。实部是一个实数，虚部是一个纯虚数。

2.数学复数的性质

数学复数的性质包括共轭性、模长、辐角等。共轭性指的是一个复数与其共轭复数相等；模长表示复数到原点的距离；辐角表示复数与正实轴之间的夹角。

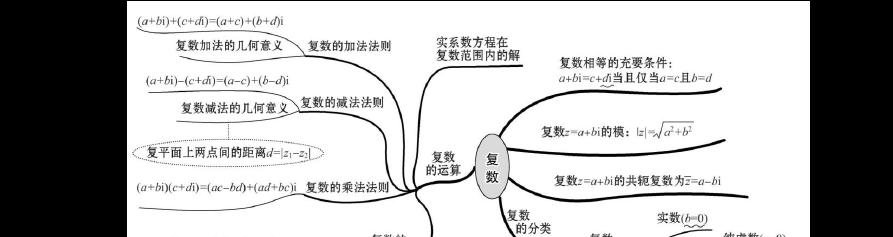
3.数学复数的表示形式

数学复数可以用代数形式、三角形式和指数形式进行表示。代数形式为a+bi，三角形式为r(cosθ+isinθ)，指数形式为re^(iθ)。

4.数学复数的四则运算

数学复数的四则运算包括加法、减法、乘法和除法。加法与减法是实部和虚部分别相加减；乘法是模长相乘，辐角相加；除法是模长相除，辐角相减。

5.数学复数的共轭与模长运算

数学复数的共轭运算是将虚部取负，得到的结果称为共轭复数；模长运算是求复数到原点的距离，即求平方根。

6.欧拉公式与数学复数

欧拉公式e^(iθ)=cosθ+isinθ是数学复数与三角函数之间的重要关系，通过欧拉公式可以将指数形式与三角形式互相转化。

7.数学复数的乘方和开方运算

数学复数的乘方运算是指将一个复数自乘若干次，开方运算是指求一个复数的平方根。这些运算可以通过欧拉公式和指数形式进行简化。

8.数学复数在坐标系中的表示

在复平面坐标系中，实轴表示实部，虚轴表示虚部，一个复数可以用一个有序数对(x,y)表示，其中x为实部，y为虚部。

9.数学复数的几何意义

数学复数可以表示平面上的点，其模长表示到原点的距离，辐角表示与正实轴之间的夹角。复数可以用来描述平面上的向量。

10.应用举例：电路中的交流电分析

数学复数在电路中的应用非常广泛，特别是交流电分析。通过将电流和电压表示为复数形式，可以简化计算过程，并得到准确的结果。

11.应用举例：信号处理中的傅里叶变换

数学复数在信号处理中的应用也十分重要，特别是傅里叶变换。傅里叶变换可以将时域信号转换为频域信号，利用复数运算进行频谱分析。

12.应用举例：量子力学中的波函数描述

数学复数在量子力学中扮演着重要的角色，波函数就是用复数表示的物理量。通过波函数描述，可以计算出粒子在空间中的各种性质。

13.数学复数与实际问题的联系

数学复数与实际问题密切相关，通过理解和应用数学复数的知识，可以解决很多实际问题，如电路分析、信号处理、量子力学等。

14.数学复数的意义与应用前景

数学复数的意义不仅体现在理论研究中，还体现在实际应用中。随着科学技术的不断发展，数学复数的应用前景将会越来越广阔。

15.

数学复数是一门重要的数学分支，掌握数学复数的基本知识对于解决实际问题具有重要意义。通过本文的介绍，相信读者能够更深入地理解和应用数学复数。

转载请注明来自数码俱乐部，本文标题：《深入理解数学复数的基本知识（探索数学复数的性质、运算及应用）》

标签：数学复数